精英公校考试Selective Entry Exam三角函数知识点解析

即将到来的精英公校考试Selective Entry Exam大家都准备好了嘛？今天我们主要来讲一讲精英公校考试Selective Entry Exam考试中，一个九年级才会涉及到的，比较新的知识点：三角函数（trigonometry）。

精英公校考试Selective Entry Exam涉及到的三角关系只针对锐角（acute angle），因此我们通常可以通过借助直角三角形来理解记忆。

一、精英公校考试Selective Entry Exam数学三角函数｜三角关系（sine，cosine，tangent）

要理解基础的三角关系，那我们需要先知道直角三角形中，什么是直角边（hypotenuse），邻边（adjacent side）和对边（opposite side）。需要注意的是，邻边和对边都是相对于我们的角θ而言的。

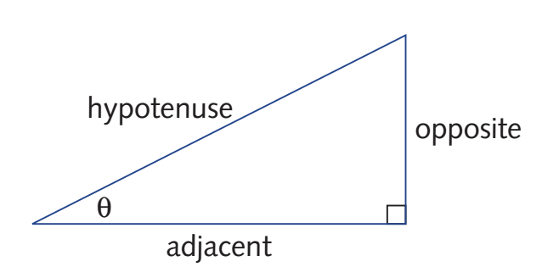
基本的锐角三角关系 （sine，cosine，tangent）都可以利用这三边的长度来定义：

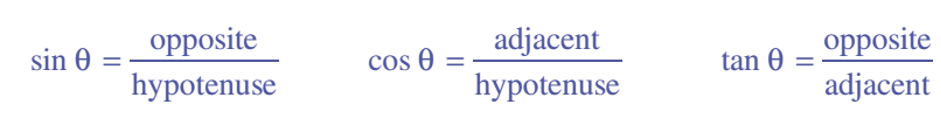
因为在直角三角形中斜边最长，因此我们可以得到以下规律，当 0<q<< span="">90°时：

0<sinθ<1

0<cosθ<1

tanθ>0

同学们在答题的时候可以利用以上规律来帮助自己快速排除错误答案。

二、精英公校考试Selective Entry Exam数学三角函数｜余角公式（complement angle formula）

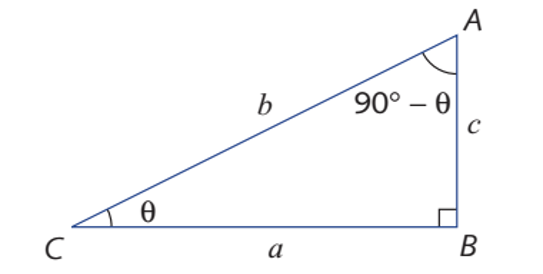
在直角三角形中，由于存在一个直角（right angle），并且三角形的内角和必定为180°，那么剩下的两个锐角相加也一定为90°，这样的两个角我们称之为互余，或者称∠CAB 为∠ACB的余角（complementary angle）。

在三角形中我们不难发现，∠CAB的邻边（c）恰好是∠ACB的对边，同时，∠CAB的对边（a）恰好是∠ACB 邻边，因此根据三角关系的定义，我们可以得到

这就是我们常说的三角函数的余角公式。

同学们在实际运用中，可以通过下图的直角三角形来帮助自己回忆和推导。

三、精英公校考试Selective Entry Exam数学三角函数｜三角函数常见题目类型

由于通常情况下，特定角度的三角函数值只能通过计算器计算，因此考试中更多是需要利用三角函数建立边角关系。我们来看一个今年practice test里出现的题目：

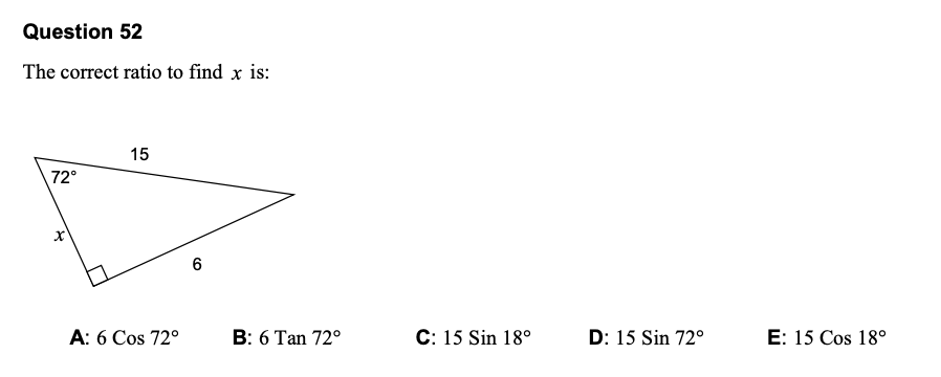
在这一个题目里，直角三角形的三个边都给到了我们，因此我们建立很多个关于x和角度的等式关系，相对于72°的这个角，它的对边（opposite）是6，邻边（adjacent）是x，斜边（hypotenuse）是15，那么我们可以得到

通过简单的移项，我们可以得到 x = 15 cos 72° 或 x = 6/tan 72°，但这两个答案都不在选项中，因此我们需要考虑利用余角（complement angle）来建立关系。我们可以很容易的利用三角形内角和180°得出，图上没有标注的另一个角为 90°-72°=18°，那么相对于这个18°的角，对边（opposite）= x，邻边（adjacent）=6，斜边（hypotenuse）=15，我们可以得到

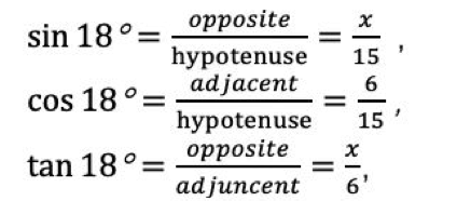
经过移项，我们得到 x = 15 sin 18° 或 x = 6 tan 18°，因此正确选项为 c.

四、精英公校考试Selective Entry Exam数学三角函数｜常见的三角函数值

我们之前也提到过，通常情况不会要求学生了解任意角度的三角函数值，但是以下三个角度的三角函数值还是需要熟悉的，分别是 30°，45°，和60°。

下图这两个直角三角形可以帮助我们很好的记忆：

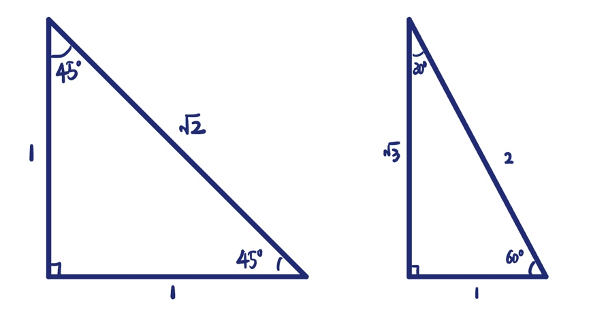
同学们只需要记住这两个三角形中，45°两直角边相等，30°对边是斜边的一半，另一条边都可以利用Pythagoras theorem来计算。

五、精英公校考试Selective Entry Exam数学三角函数｜通过三角关系确定角度（inverse trigonometric function）

这一部分同学们只需要了解inverse trigonometric function的定义就好：

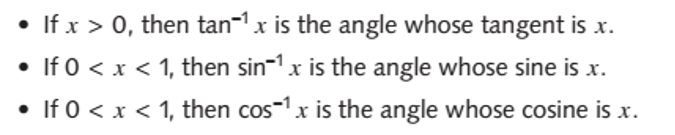
只需要认识这些符号所表达的意思即可。