美国数学竞赛AMC和AIME区别在哪里?
2022-10-09 21:18:59来源:未知作者: 飞飞阅读量:
AMC和AIME都是数学竞赛选拔性的考试,是N级别考试中,知名度比较高的考试之一。那么同是数学竞赛AMCvsAIME区别究竟在哪里?

AMC竞赛包括AMC8、AMC10/12、AIME、USAMOUSAJMO,不过后两个主要是晋级赛和美国奥数国家队选拔赛。
AMC8,主要面向8年级、14岁以下的学生,适合于想锻炼数学逻辑、培养数学兴趣的同学参加。
AMC10/12,主要面向10年级(高一)和12年级(高三)以下的高中生,适合于大学打算申请顶级名校理工类专业的同学参加。
数学竞赛都是一层层选拔,越到上层,难度越大。同样在AMC中获得了130+的分数,在AIME中可能就会产生8分和13分的区别。
因此,AMC10、12和AIME之间还有很大的不同:
01 题型不同
AMC是选择题,AIME是填空题,这就是最大的不同,这点不同,直接决定了做题方法的不同。选择题是最容易做的一种题型,起码有的选,而填空题,甚至更难的问答题或者证明题就难度大一些。既然是选择题,当然有各种可以“投机取巧”的方法。比如特殊值法、代入法、观察法等等。
02 知识点不同
AIME的大部分考点都是与AMC12一致的,此外在几何、数论、组合模块各多了少量的知识点,这些知识点大多比较复杂,一般出现在AIME的后5题中,掌握这些知识点是冲击高分的关键。但是不要忘记前10题中,多数还是AMC10和12的核心知识点,因此巩固强化AMC部分的内容也是很重要的。(注:对于AMC10首次晋级AIME的考生来讲,备考AIME首先需要了解AMC12相比AMC10所多出的内容)
AIME相比AMC12新增的核心知识点
代数:无
几何:三角形的多心问题根轴与根心塞瓦定理Masspoint方法位似变换
数论:高次同余方程指数型同余计算(指数与原根)重要数论定理(费马、欧拉、拉格朗日、威尔逊、LTE)线性不定方程乘性函数
组合:无穷状态的期望问题生成函数
AMC12相比AMC10新增的核心知识点
代数:对数三角函数复数与多项式圆锥曲线三维坐标系多重数列求和
几何:圆幂圆内接四(多)边形圆外切四边形正余弦定理Stewart定理
数论:中国剩余定理
组合:递推计数插板法
03 更加灵活和综合的题目
灵活性:AIME的题目往往都有很多的切入点,但真正适合的方法可能只有少数。例如代数部分AIME虽然没有新增的知识点,但是非常重视代数变形和计算的技巧,如特殊值、抽象化、整体代换、因式分解、递推、对称式、自相似、二元二次方程的计算技巧、赋予代数式几何含义等等。这些技巧都非常灵活,不是死记硬背就可以套用的公式,需要考生拿到题目时,进行思考、分析、尝试,找出最合适的方法。此外,几何题和组合题也有类似的特点。
综合性:AIME的很多题目都可能会涉及多个模块的知识点,以及不同的解题技巧。例如一道三角函数的题目,可能会牵扯复数和多项式的技巧以及几何的性质;一道几何的题目,可能会用复数和坐标系的方法;一道代数的题目如果有很多整数的条件,可能会和数论有很大的关系;一道概率计算的题目,可能最终是一个递推数列求解或者多重数列求和的问题。
目前AMC8虽然是针对8年级及以下的同学,不过从近两年的报告来看,低龄学生参加的人数也逐渐增加,超前通关。
如果孩子想要为申请添砖加瓦,可以根据学生的学习情况选择AMC8、10或12参加。只有通关了AMC8、10或12并达到要求后,获组委会邀请才可以参加AIME。
相关文章

AMC8竞赛的培训课程哪里有呢?怎么学习AMC8竞赛呢?
现在的家长啊,都为了孩子升学操碎了心。为了增加孩子的竞争力,不少家长都让孩子参加国际竞赛或者培养兴趣特长。其中,AMC8竞赛就受到了很多家长的...
阅读: 5

袋鼠数学竞赛课程安排,袋鼠竞赛冲刺备考攻略
开学啦,3月份一到,朋友圈里城市绿洲、星河湾的家长们就忙起来了,都忙着带孩子准备那个袋鼠数学竞赛。这个竞赛啊,对低年级学生来说,就像是参加...
阅读: 2

上海哪里可以培训AMC8竞赛呢?上海小升初认可AMC8竞赛吗?
听说AMC8竞赛在朋友圈和社交平台上都是家长们热议的话题,这个竞赛在国外很火,现在国内也超有人气的。那些打算走国际路线的孩子,都把AMC8当作进入...
阅读: 1

8年级学AMC10数学竞赛早吗?如何备考AMC101
8年级学生参加AMC10早吗?AMC10竞赛的参赛学生年龄要求在10年级以下,但因AMC10的考察知识点会超出8年级学生的数学知识范畴,因此很多家长觉得8年级学生现...
阅读: 11

AMC8竞赛12种重点题型知识板块总结
AMC8数学竞赛考什么?AMC8竞赛重点题型有哪些?对于计划参加AMC8数学竞赛的学生来说,了解竞赛题型是备考过程中很重要的 一步,本文整理了AMC8竞赛知识板块...
阅读: 30
热门文章
-
1.AMC8竞赛的培训课程哪里有呢?怎么学习AMC8竞赛呢?
- 1

- AMC8竞赛的培训课程哪里有呢?怎么学习AMC8竞赛呢?
- 2024-03-10
- 1
-
2.袋鼠数学竞赛课程安排,袋鼠竞赛冲刺备考攻略
- 2

- 袋鼠数学竞赛课程安排,袋鼠竞赛冲刺备考攻略
- 2024-03-10
- 2
-
3.上海哪里可以培训AMC8竞赛呢?上海小升初认可AMC8竞赛吗?
- 3

- 上海哪里可以培训AMC8竞赛呢?上海小升初认可AMC8竞赛吗?
- 2024-03-10
- 3
-
4.8年级学AMC10数学竞赛早吗?如何备考AMC101
- 4

- 8年级学AMC10数学竞赛早吗?如何备考AMC101
- 2023-12-22
- 4
-
5.AMC8竞赛12种重点题型知识板块总结
- 5

- AMC8竞赛12种重点题型知识板块总结
- 2023-12-22
- 5
-
6.AMC8竞赛报名即将结束 AMC8报名方式及流程说明步骤
- 6

- AMC8竞赛报名即将结束 AMC8报名方式及流程说明步骤
- 2023-12-22
- 6
-
7.袋鼠数学竞赛需要辅导吗?袋鼠数学竞赛辅导班怎么样?
- 7

- 袋鼠数学竞赛需要辅导吗?袋鼠数学竞赛辅导班怎么样?
- 2023-12-22
- 7
-
8.AMC8竞赛如何报名?AMC8竞赛难度变化趋势
- 8

- AMC8竞赛如何报名?AMC8竞赛难度变化趋势
- 2023-12-22
- 8
-
9.AMC8数学竞赛考多少能拿奖?五年级以下学生如何拿Top1%奖?
- 9

- AMC8数学竞赛考多少能拿奖?五年级以下学生如何拿Top1%奖?
- 2023-12-22
- 9
-
10.2024袋鼠数学思维挑战赛如何报名?费用及考试时间
- 10

- 2024袋鼠数学思维挑战赛如何报名?费用及考试时间
- 2023-12-22
- 10
热门图文
-

美国五项全能USAP比赛介绍/报名时间,参加USAP的意义是什么?
2022-09-18
-
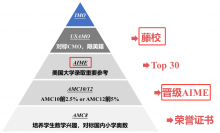
2022年AMC10新赛季开启!比赛时间及分数线分析
2022-12-05
-
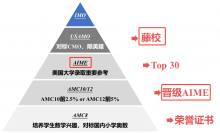
2022年AMC12数学竞赛报名及历年分数线公布
2022-12-05
-

AMC8分数线2023预测!AMC8历年分数线汇总!
2022-12-29
-

AMC报名方式(2022年AMC8/10/12竞赛中国区报名方式详解)
2022-12-05
-

2021-2022学年AMC考试报名及考试时间安排
2021-06-23
